前面我们讨论过"C#实现加权平均法",今天我们继续研究另外一种【移动加权平均法】。

在时间序列分析、股票数据处理、工业信号平滑等场景中，移动平均（Moving Average） 是最常见的平滑技术之一。相比简单移动平均（SMA），移动加权平均（WMA） 会给更靠近当前时刻的数据分配更高的权重，能更敏锐地反映趋势变化。

本文会深入了解如下内容：

• • 快速理解 WMA 的原理
• • 使用 C# 编写一个通用的 WMA 实现
• • 提供完整示例和代码解析

什么是移动加权平均（WMA）？

移动加权平均（Weighted Moving Average, WMA）与简单移动平均（Simple Moving Average, SMA）的区别在于：

• • SMA 是把窗口内的值等权重平均；
• • WMA 则对窗口内的值分配不同的权重，通常是离当前点越近，权重越大。

举个例子：

• • 对于长度为 5 的窗口，权重可能是 [1, 2, 3, 4, 5]，最新值乘以 5，最旧值乘以 1。

算法思路

对于一个时间序列：

1. 1. 定义窗口大小 n，以及对应的权重列表 [w1, w2, ..., wn]
2. 2. 从头到尾滑动窗口，每个位置计算：
3. 3. 对每个位置输出对应的 WMA。

C# 实现示例

下面是一份使用 .NET 6/C# 10 的 WMA 完整示例：

using System;
using System.Collections.Generic;
using System.Linq;

namespaceWeightedMovingAverageDemo
{
    classProgram
    {
        static void Main(string[] args)
        {
            // 原始数据序列
            List<double> data = new() { 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 };

            // 设置窗口大小
            int windowSize = 3;

            // 设置权重（例如 1, 2, 3，离当前位置越近权重越大）
            List<double> weights = new() { 1, 2, 3 };

            List<double> result = CalculateWeightedMovingAverage(data, windowSize, weights);

            Console.WriteLine("移动加权平均结果：");
            Console.WriteLine(string.Join(", ", result.Select(x => x.ToString("F2"))));
        }

        /// <summary>
        /// 计算移动加权平均数
        /// </summary>
        static List<double> CalculateWeightedMovingAverage(List<double> data, int windowSize, List<double> weights)
        {
            if (weights.Count != windowSize)
                thrownew ArgumentException("权重数量必须等于窗口大小。");

            List<double> result = new();

            for (int i = 0; i <= data.Count - windowSize; i++)
            {
                double weightedSum = 0;
                double weightSum = weights.Sum();

                for (int j = 0; j < windowSize; j++)
                {
                    weightedSum += data[i + j] * weights[j];
                }

                result.Add(weightedSum / weightSum);
            }

            return result;
        }
    }
}

代码解析

1️⃣ 输入数据

• • data：原始时间序列，如传感器数据、股价等。
• • windowSize：滑动窗口大小。
• • weights：自定义权重列表，元素个数必须与窗口大小一致。

2️⃣ 算法核心

• • 外层循环：从头到尾滑动窗口。
• • 内层循环：窗口内每个值乘以权重累加。
• • 用加权和除以权重之和，得出 WMA。

3️⃣ 返回值

• • 返回一个新的列表，长度是 data.Count - windowSize + 1。

输出结果

输入数据：

10, 20, 30, 40, 50, 60, 70, 80, 90, 100

窗口大小：3
权重：[1, 2, 3]

输出：

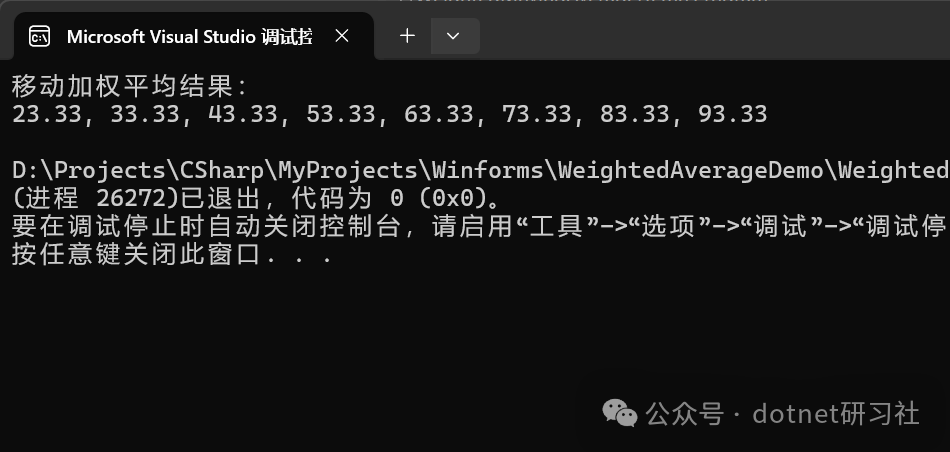解释：

• • 第一个窗口 (10,20,30) => (10×1 + 20×2 + 30×3)/6 = 23.33
• • 第二个窗口 (20,30,40) => (20×1 + 30×2 + 40×3)/6 = 33.33
• • 以此类推。

🏁 小结

本篇演示了：

• • 移动加权平均的核心原理
• • 使用 C# 编写通用实现
• • 灵活设置权重，提升趋势检测的灵敏度

在工业生产、金融数据分析、实时信号滤波等场景，都可以直接使用此实现，或者把它封装为工具类。